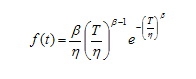Introduzione a Weibull.
Il mercato esige sempre più prodotti con qualità e prestazioni costanti nel tempo. Ovvero prodotti robusti e affidabili. Molti dei concetti affidabilistici di seguito affrontati, soprattutto di uso più frequente, sono stati presentati in [1] e in [2] ai quali si rimanda. Gli studi affidabilistici servono spesso per rispondere a domande del tipo:
qual è la vita utile di un sistema alle condizioni d'uso di 60°C?
- dopo 10.000 ore di missione alle condizioni d'uso di 60°C, quale percentuale di guasti è lecito attendersi?
- qual è la frequenza dei guasti dopo 5.700 ore di missione di un sistema?
- se il sistema ha già effettuato 7.000 ore di missione, quale percentuale di guasti è lecito attendersi nelle 3.000 ore successive?
- qual è il componente debole, meno affidabile, del sistema e quando si guasterà?
- quale piano di manutenzione si dovrebbe implementare (quando e cosa sostituire) per estendere la vita del sistema di altre 10.000 ore di missione?
- quale periodo di garanzia possiamo dare al prodotto? Possiamo estendere il periodo di garanzia previsto per legge?
- quali costi di assistenza si avranno nel periodo di garanzia?
- qual è il periodo di validità di un farmaco?
- quali sono i prodotti di degrado presenti, e la loro entità, dopo 12/24/48 mesi di vita?
Per rispondere a queste domande bisogna:
- effettuare delle prove vita e/o prove di vita accelerata;
- analizzare i dati;
- fare delle proiezioni affidabilistiche estrapolando i dati con un adeguato modello matematico.
Sicuramente le prove di vita accelerate sono molto più efficienti delle semplici prove di vita; esse possono fornire queste informazioni in pochi mesi, anziché anni, e in alcune situazioni in solo poche settimane mediante l'uso di sofisticati modelli matematici per descrivere lo stress variabile. Questi modelli matematici trasformano le prove di vita puramente qualitative, tipo "Halt & Hass", e quindi di scarsa utilità predittiva, in sofisticate prove quantitative.
In alcune situazioni ci si trova ad affrontare dei problemi di calcolo non indifferenti e si è bloccati. Di seguito vedremo come affrontare delle situazioni, le più comuni, riscontrabili nell'attività di analisi dei dati da prove vita. Molte delle applicazioni, soprattutto dove non è richiesta una grande precisione, possono essere effettuate con Excel.
L'analisi dei dati inizia con la conoscenza della distribuzione dei dati, che in questo caso sono tempi al guasto, e con la scelta della giusta distribuzione: Weibull, lognormal, esponenziale ecc. successivamente devono essere definite le modalità di estrapolazione dei dati a diversi livelli di stress.
(Tratto da: "Il manuale del Sei Sigma", di Rinaldo Tartari, Editore FrancoAngeli)
|
Distribuzione di frequenza.
Le previsioni circa la vita di un sistema inizia con l'analisi statistica dei tempi al guasto dei sottosistemi/componenti ottenuti da prove vita o da prove di vita accelerata. La distribuzione dei tempi al guasto può essere rappresentata con dei normali istogrammi e, più generalmente, con delle funzioni particolari. La più comune e utilizzabile è la distribuzione di Weibull.
La funzione di Weibull, descrive molto bene la distribuzione dei dati relativi a tempi al guasto di molti componenti e sistemi; opportunamente analizzata permette di fare delle previsioni accurate circa la vita dei componenti studiati. Il modello che presentiamo serve per descrivere le modalità di analisi statistica dei dati in situazioni facilmente riscontrabili in condizioni reali.
Una partita di 5500 pezzi, di un particolare componente, è stata montata in un lotto di elettrodomestici. Alcuni feedback dal mercato fanno capire che il componente ha una scarsa affidabilità. Infatti in una stima di circa 4000 minuti di missione sono stati effettuati circa 920 interventi. Il dubbio è se intervenire subito, con una campagna di rientri, oppure considerare i guasti già avuti come il male peggiore e quindi ritenere che quanti particolari erano destinati a guastarsi si sono già guastati nel primo periodo di vita (mortalità infantile). Una domanda d'obbligo potrebbe essere: quanti particolari guasti è lecito aspettarsi prima della scadenza del periodo di garanzia?
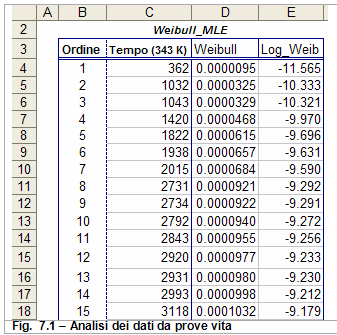
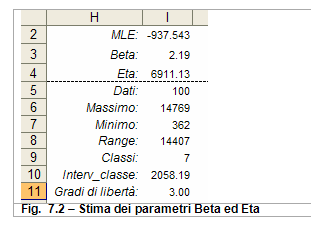
Prima della messa in uso del componente, nell'attuale configurazione, non furono effettuate delle prove di vita in quanto si considerava il componente gia affidabile dato il largo uso negli anni passati e data la disponibilità di informazioni provenienti da prove di vita accelerata effettuate alcuni anni prima. La situazione è riepilogata in tab. 7.1.
|